Internal Loadings in a Beam 2
The following module expands on the topic of two-dimensional FBD diagrams, the method of sections, and
internal forces and moments. The module illustrates homework problem 7 in chapter 7 of the 13th
edition of Hibbeler's Statics.
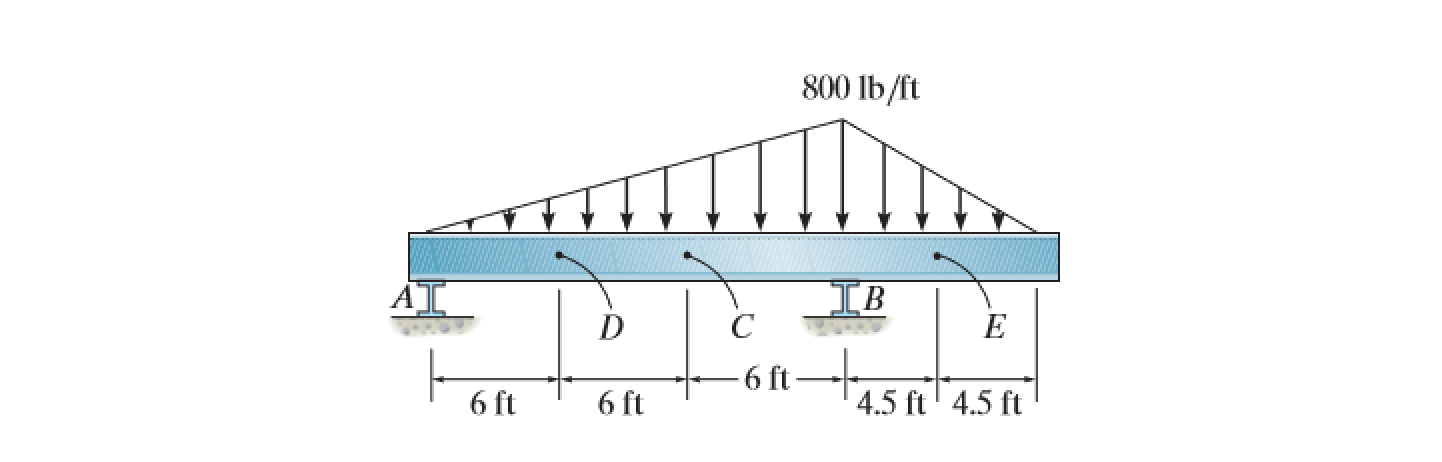
As illustrated above, a simple supported beam with a pin support at point A and roller at point B experiences both a distributed loading and external force. The problem specifically asks for internal forces and moments at C and D; however, the module shows forces and moments at all points of the beam. Determining support the reactions at A and B, it can be found that there exists no force in the x-direction. Thus, internally, the beam experiences no normal force.
Using method of sections, shear and moment equations can be found for a particular section varying with the chosen position along the beam (where x = 0 is at point A). The following module calculates and graphs shear and moment, and allows for the magnitude and location of the external force and load to be changed.
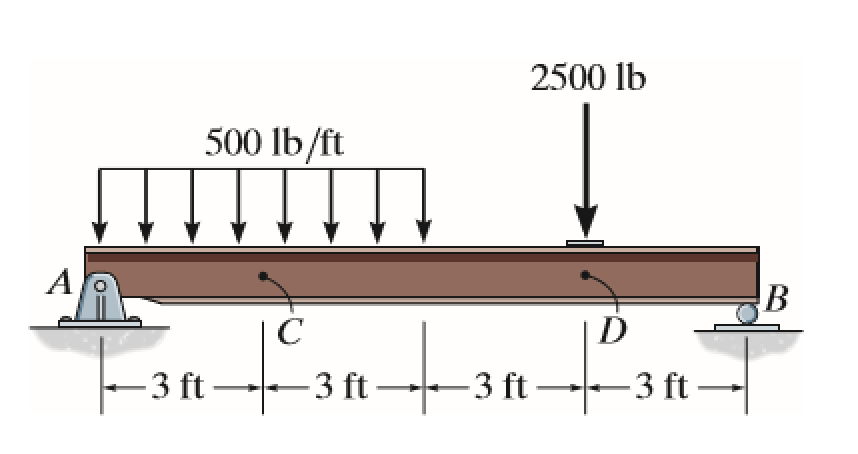
As illustrated above, a simple supported beam with a pin support at point A and roller at point B experiences both a distributed loading and external force. The problem specifically asks for internal forces and moments at C and D; however, the module shows forces and moments at all points of the beam. Determining support the reactions at A and B, it can be found that there exists no force in the x-direction. Thus, internally, the beam experiences no normal force.
Using method of sections, shear and moment equations can be found for a particular section varying with the chosen position along the beam (where x = 0 is at point A). The following module calculates and graphs shear and moment, and allows for the magnitude and location of the external force and load to be changed.